

Bulletproofs are short zero-knowledge arguments of knowledge that do not require a trusted setup.
Argument systems are proof systems with computational soundness.
Bulletproofs are suitable for proving statements on committed values, such as range proofs, verifiable suffles, arithmetic circuits, etc.
They rely on the discrete logarithmic assumption and are made non-interactive using
the Fiat-Shamir heuristic.
The core algorithm of Bulletproofs is the inner-product algorithm presented by Groth [2].
The algorithm provides an argument of knowledge of two binding vector Pedersen commitments that satisfy a given inner product relation.
Bulletproofs build on the techniques of Bootle et al. [3] to introduce a communication efficient inner-product proof that reduces
overall communication complexity of the argument to only 2log2(n) where n is the dimension
of the two vectors of commitments.
Range proofs
Bulletproofs present a protocol for conducting short and aggregatable range proofs.
They encode a proof of the range of a committed number in an inner product, using polynomials.
Range proofs are proofs that a secret value lies in a certain interval.
Range proofs do not leak any information about the secret value, other
than the fact that they lie in the interval.
The proof algorithm can be sketched out in 5 steps:
Let v be a value in [0, n) and aL a vector of bit such that <aL, 2n> = v.
The components of aL are the binary digits of v.
We construct a complementary vector aR = aL − 1n
and require that aL ◦ aR = 0 holds.
- P -> V : A, S - where A and S are blinded Pedersen commitments to aL and aR.


-
V -> P : y, z - Verifier sends challenges y and z to fix A and S.
-
P -> V : T1, T2 - where T1 and T2 are commitments to
the coefficients t1, of a polynomial t constructed from the existing values in the protocol.
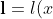&space;=&space;%5Ctextbf%7Ba%7D_L&space;-&space;z&space;%5Ccdot&space;%5Ctextbf%7B1%7D%5En&space;+&space;%5Ctextbf%7Bs%7D_L&space;%5Ccdot&space;x&space;%5Cin&space;%5Cmathcal%7BZ%7D%5En_p$)
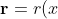&space;=&space;%5Ctextbf%7By%7D%5En&space;%5Ccirc&space;(%5Ctextbf%7Ba%7D_R&space;+&space;z&space;%5Ccdot&space;%5Ctextbf%7B1%7D%5En&space;+&space;%5Ctextbf%7Bs%7D_R&space;%5Ccdot&space;x&space;)&space;+&space;z%5E2&space;%5Ccdot&space;%5Ctextbf%7B2%7D%5En&space;%5Cin&space;%5Cmathcal%7BZ%7D%5En_p&space;$)


-
V -> P : x - Verifier challenges Prover with value x.
-
P -> V : tau, mu, t, l, r - Prover sends several commitments that the verifier will then check.


See Prover.hs for implementation details.
The interaction described is made non-interactive using the Fiat-Shamir Transform wherein all the random
challenges made by V are replaced with a hash of the transcript up until that point.
Inner-product range proof
The size of the proof is further reduced by leveraging the compact O(logn) inner product proof.
The inner-product argument in the protocol allows to prove knowledge of vectors l and r, whose inner product is t and
the commitment P ∈ G is a commitment of these two vectors. We can therefore replace sending
(tau, mu, t, l, r) with a transfer of (tau, mu, t) and an execution of an inner product argument.
Then, instead of sharing l and r, which has a communication cost of 2n elements, the inner-product
argument transmits only 2 [log2] + 2 elements. In total, the prover sends only 2 [log2(n)] + 4
group elements and 5 elements in Zp
Usage
import Bulletproofs.RangeProof
testProtocol :: Integer -> Integer -> IO Bool
testProtocol v vBlinding = do
let vCommit = commit v vBlinding
-- n needs to be a power of 2
n = 2 ^ 8
upperBound = 2 ^ n
-- Prover
proofE <- generateProof upperBound v vBlinding
-- Verifier
case proofE of
Left err -> panic $ show err
Right (proof@RangeProof{..})
-> pure $ verifyProof upperBound vCommit proof
The dimension n needs to be a power of 2.
This implementation offers support for the SECp256k1 curve, a Koblitz curve.
Further information about this curve can be found in the Uplink docs:
SECp256k1 curve
References:
-
Bunz B., Bootle J., Boneh J., Poelstra A., Wuille P., Maxwell G.
"Bulletproofs: Short Proofs for Confidential Transactions and More". Stanford, UCL, Blockstream, 2017
-
Groth J. "Linear Algebra with Sub-linear Zero-Knowledge Arguments". University College London, 2009
-
Bootle J., Cerully A., Chaidos P., Groth J, Petit C. "Efficient Zero-Knowledge Arguments for
Arithmetic Circuits in the Discrete Log Setting". University College London and University of Oxford, 2016.
Notation:
- ◦ : Hadamard product
- <> :Inner product
- a: Vector
License
Copyright 2018 Adjoint Inc
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.


