unm-hip: A Library for the manipulation of images
The University of New Mexico's Haskell Image Processing library contains functionality for performing manipulations on binary, grayscale, color, and complex images. The library was designed for use in UNM's Digital Image Processing class but it can be used for a wide range of image processing purposes.
- Changes
- unm-hip-0.0.0.2
Adjusted the label function to reduce to the lowest label values. This results in "better" output for areas, boundingBoxes, and centersOfMass
Added the Arithmetic module that provides support for arithmetic operations on images using scalar values.
- unm-hip-0.0.0.1
Added an error if fft or ifft are used with a non power of 2 image
Fixed error in equivalence labeling in label
Made consistent if and only if through out documentation
Fixed typo in Complex.hs haddock under fft.
- unm-hip-0.0.0.0
Initial release containing functionality for Boxed Images
[Skip to Readme]

Modules
[Index]
Downloads
- unm-hip-0.0.0.2.tar.gz [browse] (Cabal source package)
- Package description (as included in the package)
Maintainer's Corner
For package maintainers and hackage trustees
Candidates
- No Candidates
| Versions [RSS] | 0.0.0.0, 0.0.0.1, 0.0.0.2, 0.0.0.3, 0.1.1.4, 0.1.1.5, 0.2.1.5, 0.3.1.5, 0.3.1.6 |
|---|---|
| Change log | changes.txt |
| Dependencies | array (>=0.4.0.1), base (>=4 && <5), bytestring (>=0.10.0.2), containers (>=0.5.0.0), process (>=1.1.0.2), vector (>=0.10.0.1) [details] |
| License | LicenseRef-GPL |
| Author | Joseph Collard, Stephen Patel, Lance Williams |
| Maintainer | josephmcollard+unm-hip@gmail.com |
| Category | Image Processing |
| Source repo | head: git clone https://github.com/jcollard/unm-hip |
| Uploaded | by JosephCollard at 2013-07-15T15:41:58Z |
| Distributions | |
| Reverse Dependencies | 1 direct, 0 indirect [details] |
| Downloads | 6822 total (0 in the last 30 days) |
| Rating | (no votes yet) [estimated by Bayesian average] |
| Your Rating |
|
| Status | Docs uploaded by user Build status unknown [no reports yet] |
Readme for unm-hip-0.0.0.2
[back to package description]The University of New Mexico's Haskell Image Processing Library
To get started, import Data.Image or Data.Image.Boxed.
To use unm-hip interactively in ghci, import Data.Image.Interactive. This provides three useful functions: display, setDisplayProgram, and plotHistograms.
setDisplayProgram :: String -> Bool -> IO ()
Sets the program to use when making a call to display and specifies if the program can accept an image via stdin. If it cannot, then a temporary file will be created and passed as an argument instead. By default, ImageMagick (display) is the default program to use and it is read using stdin.
*Main> setDisplayProgram "gimp" False *Main> setDisplayProgram "xv" False *Main> setDisplayProgram "display" True
display :: DisplayFormat df => df -> IO (Handle, Handle, Handle, ProcessHandle)
Makes a call to the current display program to be displayed. If the program cannot read from standard in, a file named .tmp-img is created and used as an argument to the program.
makeImage :: Image i => Int -> Int -> PixelOp (Pixel i) -> i
Given an Int m, Int n, and a PixelOp f, makeImage returns an Image with dimensions m x n and the Pixel value at each (i, j) is (f i j)
*Main> let grad = makeImage 128 128 (\ r c -> fromIntegral (r + c)) :: GrayImage *Main> grad < Image 128x128 > *Main> display grad

pii :: Complex Double pii = 0 :+ pi harmonicSignal :: Double -> Double -> Int -> Int -> Complex Double harmonicSignal u v m n = exp ((2*pii) * ((u*(fromIntegral m) + v*(fromIntegral n)) :+ 0)) *Main> let signal = makeImage 128 128 (harmonicSignal (3 / 128) (2 / 128)) :: ComplexImage *Main> signal *Main> signal < Image 128x128 > *Main> display signal

readImage :: FilePath -> IO GrayImageGiven the file path to a file containing an image stored in ASCII .pgm format, readImage reads the file and returns the Image. For example,
*Main> frog <- readImage "images/frog.pgm" *Main> display frog

writeImage :: DisplayFormat df => FilePath -> df -> IO ()
Given a filename and an Image, writeImage creates a file representing the image in ASCII .pgm format for GrayImages and .ppm for ColorImage and ComplexImage. Note: Images saved this way are normalized to integers in the range 0 to 255; this may result in loss of detail.
*Main> writeImage "frog.pgm" frog
creates a file which looks like this:
P2 242 225 255 151 151 151 151 151 150 150 149 148 147 146 145 145 142 142 143 145 148 152 156 158 159 159 159 159 157 155 152 150 153 152 151 149 149 149 149 150 149 149 149 149 149 149 149 149 149 146 144 141 138 136 133 132 136 136 136 136 136 136 136 136 139 138 138 138 137 136 136 136 135 135 136 136 137 137 138 138 138 137 138 137 138 137 138 137 135 134 134 134 138 141 147 150 149 147 143 138 134 132 131 130 129 129 130 132 134 136 137 137 137 137 138 139 142 145 147 149 145 146 150 153 156 159 161 163 156 158 161 163 167 170 174 175 181 183 . . .
ref :: Image i => i -> Int -> Int -> Pixel i
Given an image, a positive int i, and a positive int j, ref returns the pixel value at location (i, j).
*Main> ref frog 100 100 56.0
ref' :: ref' :: GrayImage -> Double -> Double -> Double
Given a GreyImage, a positive double i, and a positive double j, ref returns the bilinear interpolated pixel value at location (i, j).
*Main> ref frog 100 100 56.0
rows :: Image i => i -> Int
Given an image, rows returns the number of rows of in the image. For example,
*Main> rows frog 225
cols :: Image i => i -> Int
Given an image, cols returns the number of columns of in the image. For example,
*Main> cols frog 242
transpose :: Image img => img -> img
Given an Image img, transpose returns an image created by interchanging the rows and columns of the image, i.e., the value at location (i, j) of the result image is the value of the img at location (j, i). For example,
*Main> transpose frog < Image 242x225 > *Main> display . transpose $ frog

convolveRows :: (Num (Pixel img), Image img) => [Pixel img] -> img -> img
Given a list consisting solely of pixel values representing a 1D convolution kernel and an image, convolveRows returns the 1D discrete periodic convolution of the rows of the image with the kernel. For example,
*Main> convolveRows [1, -1] frog < Image 225x242 > *Main> display . convolveRows [1, -1] $ frog

convolveCols :: (Num (Pixel img), Image img) => [Pixel img] -> img -> img
Given a list consisting solely of pixel values representing a 1D convolution kernel and an image, convolveCols returns the 1D discrete periodic convolution of the columns of the image with the kernel. For example,
*Main> convolveCols [1, -1] frog < Image 225x242 > *Main> display . convolveCols [1, -1] $ frog

*Main> let dx = convolveRows [1, -1] frog *Main> let dy = convolveCols [1, -1] frog *Main> let grad = imageMap sqrt ((dx * dx) + (dy * dy)) :: GrayImage *Main> grad < Image 225x242 > *Main> display grad

convolve :: (Num (Pixel img), Image img) => [[Pixel img]] -> img -> img
Given a 2D list consisting solely of pixels representing a 2D convolution kernel and an image, convolve returns the 2D discrete periodic convolution of the image with the kernel. For example,
*Main> convolve [[1, 1, 1], [1, -8, 1], [1, 1, 1]] frog < Image 225x242 > *Main> display . convolve [[1, 1, 1], [1, -8, 1], [1, 1, 1]] $ frog>

downsampleCols :: Image img => img -> img
Given img, downsampleCols returns the image created by discarding the odd numbered rows, i.e., the value at location (i, j) of the result image is the value of img at location (2i, j).
For example,
*Main> downsampleCols frog < Image 112x242 > *Main> display . downsampleCols $ frog

downsampleRows :: Image img => img -> img
Given img, downsampleRows returns the image created by discarding the odd numbered columns, i.e., the value at location (i, j) is the value of img at location (i, 2j).
For example,
*Main> downsampleRows frog < Image 225x121 > *Main> display . downsampleRows $ frog

downsample :: Image img => img -> img
*Main> let tinyFrog = downsample frog *Main> tinyFrog < Image 112x121 > *Main> display tinyFrog

upsampleCols :: (Monoid (Pixel img), Image img) => img -> img
Given img, upsampleCols returns an image with twice the number of rows where the value at location (i, j) of the result image is the value of img at location (i/2, j) if i is even and mempty otherwise.
For example,
*Main> upsampleCols tinyFrog < Image 224x121 > *Main> display . upsampleCols $ tinyFrog

upsampleRows :: (Monoid (Pixel img), Image img) => img -> img
Given img, upsampleRows returns an image with twice the number of columns where the value at location (i, j) of the result image is the value of img at location (i, j/2) if j is even and mempty otherwise.
For example,
*Main> upsampleRows tinyFrog < Image 112x242 > *Main> display . upsampleRows $ tinyFrog

upsample :: (Monoid (Pixel img), Image img) => img -> img
Given img, upsample returns an image with twice the number of rows and columns where the value at location (i, j) of the resulting image is the value of img at location (i/2, j/2) if i and jare are even and mempty otherwise.
For example,
*Main> upsample tinyFrog < Image 224x242 > *Main> display . upsample $ tinyFrog
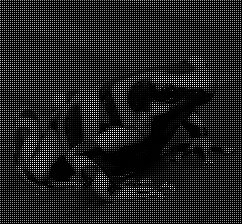
pad :: (Monoid (Pixel img), Image img) => Int -> Int -> img -> img
Given m, n, and img, pad returns an Image with m rows and n columns where the value at location (i, j) of the result image is the value of img at location (i, j) if i is less than m and j is less than n and mempty otherwise.
For example,
*Main> pad 200 200 tinyFrog < Image 200x200 > *Main> display . pad 200 200 $ tinyFrog

crop :: Image img => Int -> Int -> Int -> Int -> img -> img
Given a i0, j0, m, n, and img, crop returns an image with m rows and n columns where the value at location (i, j) of the result image is the value of img at location (i0 + i, j0 + j).
For example,
*Main> let frogPart = crop 64 64 128 128 frog *Main> frogPart < Image 128x128 > *Main> display frogPart

leftToRight :: Image img => img -> img -> img
Given two images with the same number of rows X and Y, leftToRight returns an image that is the concatenation of the two images from left to right. There is a convenience function, leftToRight' that takes a pair, triple, or list of images and displays them left to right.
For example,
*Main> leftToRight tinyFrog tinyFrog < Image 112x242 > *Main> display . leftToRight tinyFrog $ tinyFrog

topToBottom :: Image img => img -> img -> img
Given two images with the same number of columns X and Y, topToBottom returns an image that is the concatenation of the two images from top to bottom. There is a convenience function, topToBottom' that takes a pair, triple, or list of images and displays them top to bottom.
For example,
*Main> topToBottom tinyFrog tinyFrog < Image 224x121 > *Main> display . topToBottom tinyFrog $ tinyFrog

makeFilter :: Image img => Int -> Int -> PixelOp (Pixel img) -> img
Given a positive integer m, a positive integer n, and a function returning a pixel value, makeFilter returns an image with m rows and n columns. Let x equal i if i is less than m/2 and i - m otherwise and let y equal j if j is less than n/2 and j - n otherwise. To match the periodicity of the 2D discrete Fourier spectrum, the value of the result image at location (i, j) is computed by applying the function to x and y, e.g., the value at location (0, 0) is the result of applying the function to 0 and 0, the value at (m-1, n-1) is the result of applying function to -1 and -1.
For example,
*Main Data.Complex> let filter = makeFilter 128 128 (\ i j -> fromIntegral (i + j)) :: GrayImage *Main Data.Complex> filter < Image 128x128 > *Main Data.Complex> display filter

laplacianOfGaussian stddev i j =
let r = fromIntegral (i*i + j*j)
x = (r / 2.0) / stddev
in (((-pi) / stddev) / stddev) * (1 - x) * (exp (-x))
*Main Data.Complex> let d2g = makeFilter 128 128 (laplacianOfGaussian 8) :: ComplexImage
*Main Data.Complex> d2g
< Image 128x128 >
*Main Data.Complex> display d2g

fft :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Complex (Value (Pixel img))) => img -> img'
Given an image whose pixels can be converted to a complex value,
fft returns an image with complex pixels representing its 2D discrete
Fourier transform (DFT). Because the DFT is computed using the Fast Fourier
Transform (FFT) algorithm, the number of rows and columns of the image
must both be powers of two, i.e., 2K where K is an integer.
For example,
*Main> let logFrog = magnitude . imageMap log . fft $ frogpart
*Main> logFrog
< Image 128x128 >
*Main> display logFrog

*Main> fft d2g
< Image 128x128 >
*Main> display . fft $ d2g

gaussian variance i j =
let r = fromIntegral (i*i + j*j)
x = (r / (2*pi)) / variance
in exp (-x)
*Main> let g = makeFilter 128 128 (gaussian 8) :: GrayImage
*Main> display g

*Main> fft g
< Image 128x128 >
*Main> display . fft $ g

ifft :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Complex (Value (Pixel img))) => img -> img'
Given an image, ifft returns a complex image representing its 2D
inverse discrete Fourier transform (DFT). Because the inverse DFT is
computed using the Fast Fourier Transform (FFT) algorithm, the number
of rows and columns of must both be powers of two, i.e., 2K
where K is an integer.
For example,
*Main> ifft ((fft frogPart) * (fft d2g))
< Image 128x128 >
*Main> display $ ifft ((fft frogPart) * (fft d2g))

*Main> ifft ((fft frogPart) * (fft g))
< Image 128x128 >
*Main> display $ ifft ((fft frogPart) * (fft g))

realPart :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Value (Pixel img)) => img -> img'
Given a complex image, returns a real image representing
the real part of the image.
For example,
*Main> let cosine = realPart signal :: GrayImage
*Main> cosine
< Image 128x128 >
*Main> display cosine

*Main> display . realPart . ifft $ (fft frogpart) * (fft d2g)

*Main> display . realPart . ifft $ (fft frogpart) * (fft g)
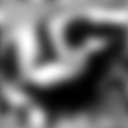
imagPart :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Value (Pixel img)) => img -> img'
Given a complex image, imagPart returns a real image representing
the imaginary part of the image
For example,
*Main> let sine = imagPart signal :: GrayImage
*Main> sine
< Image 128x128 >
*Main> display sine

complex :: (Image img, Image img', Pixel img' ~ C.Complex (Pixel img)) => img -> img -> img'
Given an image representing the real part of a complex image, and
an image representing the imaginary part of a complex image, complex returns
a complex image.
For example,
*Main> complex cosine sine :: ComplexImage
< Image 128x128 >
*Main> display (complex cosine sine :: ComplexImage)

complexImageToRectangular :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Value (Pixel img)) => img -> (img', img')
Given a complex image, complexImageToRectangular returns a pair of real images each representing
a component of the complex image (real, imaginary).
For example,
*Main> leftToRight' . complexImageToRectangular $ signal
< Image 128x256 >
*Main> display . leftToRight' . complexImageToRectangular $ signal

magnitude :: (Image img, Image img', ComplexPixel (Pixel img), Pixel img' ~ Value (Pixel img)) => img -> img'
Given a complex image, returns a real image representing
the magnitude of the image.
angle :: (Image img, ComplexPixel (Pixel img), Image img', Pixel img' ~ Value (Pixel img)) => img -> img'
Given a complex image, angle returns a real image representing
the angle of the image.
For example,
*Main> angle signal
< Image 128x128 >
*Main> display (angle signal :: GrayImage)

complexImageToPolar :: (Image img, ComplexPixel (Pixel img), Image img', Pixel img' ~ Value (Pixel img)) => img -> (img', img')
Given a complex image, complexImageToPolar returns a pair of real images each
representing the component (magnitude, phase) of the image
*Main> complexImageToPolar signal
(< Image 128x128 >,< Image 128x128 >)
*Main> display . leftToRight' . complexImageToPolar $ signal

(==) :: (==) :: Eq a => a -> a -> Bool
Images installed in the Eq type class (Boxed images) may be compared using the (==). This returns True if and only iff the images are of equal dimension and for each pixel (i, j) in the two images are (==).
(<) :: Ord a => a -> a -> Bool
Images installed in the Ord type class (Boxed images) may be compared using (<). This returns True if and only iff the images are of equal dimension and for each pixel (i, j) in the two images are (<).
(>) :: Ord a => a -> a -> Bool
Images installed in the Ord type class (Boxed images) may be compared using (>). This returns True if and only iff the images are of equal dimension and for each pixel (i, j) in the two images are (>).
(+) :: Num a => a -> a -> a
Any two images installed in the Num type class (any two Boxed images) may be added if their dimensions match.
For each (i, j) the resulting pixel will be the sum of the pixels from the given images.
For example,
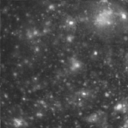
*Main> callisto <- readImage "images/callisto.pgm"
*Main> display callisto
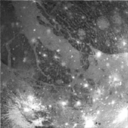
*Main> ganymede <- readImage "images/ganymede.pgm"
*Main> display ganymede
*Main> callisto + ganymede
< Image 128x128 >
*Main> display $ callisto + ganymede

(-) :: Num a => a -> a -> a
Any two images installed in the Num type class (any two Boxed images) may be subtracted if their dimensions match.
For each (i, j) the resulting pixel will be the difference of the two pixels from the given images.
For example,
*Main> display $ callisto - ganymede

(*) :: Num a => a -> a -> a
Any two images installed in the Num type class (any two Boxed images) may be multiplied if their dimensions match.
For each (i, j) the resulting pixel will be the product of the two pixels from the given images.
For example,
*Main> display (callisto * ganymede)
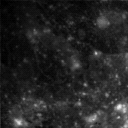
(/) :: Fractional a => a -> a -> a
Any two images installed in the Num type class (any two Boxed images) may be divided if their dimensions match.
For each (i, j) the resulting pixel will be the quotient of the two pixels from the given images.
For example,
*Main> display (callisto / ganymede)
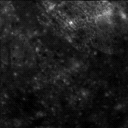
arrayToImage :: Image img => Array (Int, Int) (Pixel img) -> img
Given a two dimensional array of Pixel values indexed by
pairs of Ints where the fst is the row and snd is the column, arrayToImage returns
an Image.
For example,
*Main> let array = listArray ((0,0),(127,127)) [0..] :: Array (Int,Int) Double
*Main> arrayToImage array :: GrayImage
< Image 128x128 >
*Main> display (arrayToImage array :: GrayImage)

imageToArray :: Image img => img -> Array (Int, Int) (Pixel img)
Given img, imageToArray returns an two dimensional array of Pixel values
indexed by pairs of Ints where the fst is the row and snd is the column.
*Main> let arr = listArray ((0,0),(2,2)) [0..] :: Array (Int, Int) Double
*Main> imageToArray (arrayToImage arr :: GrayImage)
array ((0,0),(2,2)) [((0,0),0.0),((0,1),1.0),((0,2),2.0),((1,0),3.0),((1,1),4.0),((1,2),5.0),((2,0),6.0),((2,1),7.0),((2,2),8.0)]
(>.) :: (Ord (Pixel img), Image img, BinaryPixel (Pixel img)) => Pixel img -> img -> img
Given a Pixel p and an image img, return a Binary image where the
pixel at (i, j) is on if p is greater than the corresponding pixel in
img at (i,j) and off otherwise.
Note: there is a variation of (.<) named (>.) where the arguments are flipped.
(>~) :: (Ord (Pixel img), Image img) => Pixel img -> img -> Bool
Given a pixel value p and an image img, return True if and only if all
values in img are less than p.
Note: there is a variation of (>~) named (~<) where the arguments are flipped.
*Main> stop <- readColorImage "images/stop.ppm"
*Main> display stop

*Main> let (r,g,b) = colorImageToRGB stop
*Main> let binaryStop = (r + g + b) .> 400
*Main> display binaryStop

(<.) :: (Ord (Pixel img), Image img, BinaryPixel (Pixel img)) => Pixel img -> img -> img
Given a Pixel p and an image img, return a Binary image where the
pixel at (i, j) is on if p is less than the corresponding pixel in
img at (i,j) and off otherwise.
Note: there is a variation of (<.) named (.<) where the arguments are flipped.
*Main> let binaryStop = (r + g + b) .< 400
*Main> display binaryStop

(<~) :: (Ord (Pixel img), Image img) => Pixel img -> img -> Bool
Given a pixel value p and an image img, return True if and only if all
values in img are greater than p.
Note: there is a variation of (<~) named (~<) where the arguments are flipped.
(.==.) :: (Eq (Pixel img), Image img, BinaryPixel (Pixel img)) => img -> img -> img
Given an image with pixels, p, and a pixel, c, returns an image where
each pixel has the value 1 if and only iff p = c and 0 otherwise.
Note: there is a variation of (==.) named (.==) in which each pixel in the image is compared to a single specified Pixel.
shiftRight :: Image img => Int -> img -> img
shiftRight s img = makeImage (rows img) (cols img) shift where
shift r c = ref img r c' where
c' = let sum = c + s
in if sum < (cols img) then sum else sum - (cols img)
*Main> let binaryStop = (r + g + b) .> 400
*Main> display $ (shiftRight 100 binaryStop)

*Main> display $ (shiftRight 100 binaryStop) .==. binaryStop

normalize :: (Fractional (Pixel img), MaxMin (Pixel img), Image img) => img -> img
Given img, normalize returns an image with the same dimensions
where the values have been normalized to lie in the interval [0, 1].
shrink :: (Num a, Image img, ComplexPixel (Pixel img), Image img', Pixel img' ~ C.Complex (Value (Pixel img))) => a -> img -> img'
Given a complex image and a real positive number x, shrink returns
a complex image with the same dimensions. Let z be the value of the
image at location (i, j). The value of the complex result image at
location (i, j) is zero if |z| < x, otherwise the result has the
same phase as z but the amplitude is decreased by x.
medianFilter :: (Ord (Pixel img), Image img) => Int -> Int -> img -> img
Given two positive integers, m and n and a an image,
medianFilter returns an image with the same dimensions where each
pixel (i, j) in is replaced by the pixel with median value
in the neighborhood of size m times n centered on (i, j).
*Main> let medianFilteredFrog = medianFilter 5 5 frog
*Main> display medianFilteredFrog

imageFold :: Image img => (Pixel img -> b -> b) -> b -> img -> b
Given a function of a pixel to a value of type b which
returns a value of type b, imageFold
returns the value of type b which results
from repeatedly applying the function to: 1) the result
accumulated to this point (initially the value of the first pixel);
and 2) the value of the next pixel.
matrixProduct :: (Num (Pixel img), Image img) => img -> img -> img
Given an image X1 and an image X2, where the number of columns of X1
equals the number of rows of X2, matrixProduct returns an image
representing the matrix product of X1 and X2.
*Main> display (matrixProduct frogPart frogPart)

imageMap :: (Image a, Image b) => (Pixel a -> Pixel b) -> a -> b
Given a function of a pixel value of type a to a pixel value of type
b, and an image containing pixel values of type a,
imageMap returns an image of type b where each pixel in the result
image is the result of appyling the function to each pixel in the given image.
Note: Boxed images are in typeclass Functor and Applicative it
is recommended you use fmap instead of imageMap for Boxed images.
*Main> let img = imageMap ((-1) *) frog :: GrayImage
*Main> display img

readColorImage :: FilePath -> IO ColorImage
Given the file path to a file containing an image
stored in ASCII .ppm format, readColorImage reads the
file and returns the ColorImage
For example,
*Main> cacti <- readColorImage "images/cactii.ppm"
*Main> display cacti

colorImageRed :: ColorImage -> GrayImage
Given a ColorImage, colorImageRed returns a GrayImage representing the Red color component
For example,
*Main> let red = colorImageRed cacti
*Main> display red

colorImageGreen :: ColorImage -> GrayImage
Given a ColorImage, colorImageGreen returns a GrayImage representing the Green color component
For example,
*Main> let green = colorImageGreen cacti
*Main> display green

colorImageBlue :: ColorImage -> GrayImage
Given a ColorImage, colorImageBlue returns a GrayImage representing the Blue color component
For example,
*Main> let blue = colorImageBlue cacti
*Main> display blue

rgbToColorImage :: (GrayImage, GrayImage, GrayImage) -> ColorImage
Given a triple containing three GrayImages each containing one of the
color components (red, green, blue), rgbToColorImage returns a ColorImage
*Main> display . rgbToColorImage $ (red,green,blue)

colorImageToRGB :: ColorImage -> (GrayImage, GrayImage, GrayImage)
Given a ColorImage, colorImageToRGB returns a triple containing three GrayImages each
containing one of the color components (red, green, blue)
For example,
*Main> display . leftToRight' $ colorImageToRGB cacti

colorImageToHSI :: ColorImage -> (GrayImage, GrayImage, GrayImage)
Given a ColorImage, colorImageToHSI returns a triple containing three GrayImages each
containing one of the components (hue, saturation, intensity)
For example,
*Main> let (h,s,i) = colorImageToHSI cacti
*Main> display h

*Main> display s

*Main> display i

hsiToColorImage :: (GrayImage, GrayImage, GrayImage) -> ColorImage
Given a triple containing three GrayImages each containing one of the
color components (hue, saturation, intensity), hsiToColorImage returns a ColorImage
For example,
*Main> display . hsiToColorImage $ (h, s, i)

makeHotImage :: GrayImage -> ColorImage
Given a GrayImage, makeHotImage returns a ColorImage with the same
dimensions. The R, G, B values of the result image at (i, j) are
determined by using the value of the ColorImage at (i, j) to index
three lookup tables. These lookup tables implement a false coloring
scheme which maps small values to black, large values to white, and
intermediate values to shades of red, orange, and yellow (in that order).
*Main> display . makeHotImage $ frog

dilate :: (Eq (Pixel img), Num (Pixel img), Image img, BinaryPixel (Pixel img)) => [[Pixel img]] -> img -> img
Given a 2D list consisting solely of pixels representing a structuring
element, and a binary image, dilate returns the morphological dilation of
the with the structuring element.
Note: There is a dilate' function that uses a default
structuring element of [[1,1], [1,1]]. For example,
structure = [[0, 0, 1, 0, 0],
[0, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0]]
*Main> display . dilate structure $ binaryStop

erode :: (Eq (Pixel img), Num (Pixel img), Image img, BinaryPixel (Pixel img)) => [[Pixel img]] -> img -> img
Given a 2D list consisting solely of pixels representing a structuring
element, and a binary image, erode returns the morphological erosion of
the with the structuring element.
Note: There is a erode' function that uses a default structuring element of [[1,1], [1,1]].
For example,
*Main> display . erode structure $ binaryStop

outline :: (Image img, BinaryPixel (Pixel img), Eq (Pixel img)) => img -> img
Given an image, outline returns an image where edge pixels are
set to the value on and non-edge pixels are set to the value off.
Pixel (i, j) is an edge pixel if and only iff its value is different than the value
of either pixel (i, j+1) or pixel (i+1, j).
Note: There is an outline' that allows the for the non-edge and edge pixel values to be specified.
*Main> display . outline $ binaryStop

label :: (Image img, BinaryPixel (Pixel img)) => img -> GrayImage
Given a binary image, label returns an image where pixels in
distinct connected components (based on 4-neighbor connectivity)
have distinct integer values. These values range from 1 to n where
n is the number of connected components in image.
*Main> display . makeHotImage . label $ binaryStop

distanceTransform :: (Image img, BinaryPixel (Pixel img)) => img -> GrayImage
Given a binary image, distanceTransform returns an image
representing the 2D distance transform of the image.
The distance transform is accurate to within a 2% error for euclidean
distance.
*Main> display . distanceTransform . dilate $ binaryStop

open :: (Eq (Pixel img), Num (Pixel img), Image img, BinaryPixel (Pixel img)) => [[Pixel img]] -> img -> img
Given a 2D list consisting solely of pixels representing a structuring
element, and a binary image, open returns the morphological opening of
the image with the structuring element.
Note: There is a version open' that uses the default structuring element [[1,1],[1,1]].
Main*> noise <- readColorImage "images/noise.ppm"

Main*> let noisyStop = binaryStop ./=. noise

Main*> display . open $ noisyStop

close :: (Eq (Pixel img), Num (Pixel img), Image img, BinaryPixel (Pixel img)) => [[Pixel img]] -> img -> img
Given a 2D list consisting solely of pixels representing a structuring
element, and a binary image, close returns the morphological closing of
the image with the structuring element.
Note: There is a version close' that uses the default structuring element [[1,1],[1,1]].
Main*>close [[1,1],[1,1]] noisyStop

areas :: (Image img, MaxMin (Pixel img), RealFrac (Pixel img)) => img -> V.Vector Double
Given an image, areas returns a vector where the n-th component equals
the number of pixels with value n. If image is the result of applying
label to a binary image, then the vector represents the areas of the
connected-components of the binary-image. If not, areas returns
the histogram of the image.
For example,
*Main> areas . label $ binaryStop
fromList [9240.0,1154.0,1326.0,809.0,1145.0]
perimeters :: (Image img, MaxMin (Pixel img), Pixel img ~ Double) => img -> V.Vector Double
Given an image, perimeters returns a vector where the n-th component
equals the number of pixels with value n which are adjacent to pixels
of value 0 and the 0-th component equals the sum of the other components.
If image is the result of applying label to a binary image, then the
vector represents the perimeters of the connected-components of the
binary-image.
For example,
*Main> perimeters . label $ binaryStop
fromList [1082.0,312.0,326.0,184.0,260.0]
centersOfMass :: (Image img, MaxMin (Pixel img), Pixel img ~ Double) => img -> [(Double, Double)]
Given an image, the result of applying label to a binary-image,
centersOfMass returns a vector where the n-th component is a tuple
representing the average row and column indices of pixels of the
n-th connected-component of the image.
For example,
*Main> centersOfMass . label $ binaryStop
[(42.2686308492201,24.657712305025996),(41.74660633484163,92.20889894419307),(35.31025957972806,57.595797280593324),(35.583406113537116,129.9170305676856)]
boundingBoxes :: (Image img, MaxMin (Pixel img), Pixel img ~ Double) => img -> [(Int, Int, Int, Int)]
Given an image, the result of applying label to a binary-image,
boundingBoxes returns a vector where the n-th component is a four
element tuple representing the minimum and maximum row and column
indices of pixels of the n-th connected-component of the image.
For example,
*Main> boundingBoxes . label $ binaryStop
[(10,8,73,41),(10,75,74,110),(11,42,72,73),(11,117,72,150)]