| Copyright | (c) Masahiro Sakai 2011-2019 |
|---|---|
| License | BSD-style |
| Maintainer | masahiro.sakai@gmail.com |
| Stability | provisional |
| Portability | non-portable |
| Safe Haskell | Safe-Inferred |
| Language | Haskell2010 |
| Extensions |
|
Numeric.Optimization.MIP.Base
Description
Mixed-Integer Programming Problems with some commmonly used extensions
Synopsis
- data Problem c = Problem {
- name :: Maybe Text
- objectiveFunction :: ObjectiveFunction c
- constraints :: [Constraint c]
- sosConstraints :: [SOSConstraint c]
- userCuts :: [Constraint c]
- varDomains :: Map Var (VarType, Bounds c)
- variables :: Problem c -> Set Var
- continuousVariables :: Problem c -> Set Var
- integerVariables :: Problem c -> Set Var
- binaryVariables :: (Num c, Eq c) => Problem c -> Set Var
- semiContinuousVariables :: Problem c -> Set Var
- semiIntegerVariables :: Problem c -> Set Var
- varTypes :: Problem c -> Map Var VarType
- varType :: Problem c -> Map Var VarType
- getVarType :: Problem c -> Var -> VarType
- varBounds :: Problem c -> Map Var (Bounds c)
- getBounds :: Num c => Problem c -> Var -> Bounds c
- data Var where
- varName :: Var -> Text
- toVar :: String -> Var
- fromVar :: Var -> String
- data VarType
- type BoundExpr c = Extended c
- data Extended r
- type Bounds c = (BoundExpr c, BoundExpr c)
- defaultBounds :: Num c => Bounds c
- defaultLB :: Num c => BoundExpr c
- defaultUB :: BoundExpr c
- type Label = Text
- data Expr c where
- varExpr :: Num c => Var -> Expr c
- constExpr :: (Eq c, Num c) => c -> Expr c
- terms :: Expr c -> [Term c]
- data Term c = Term c [Var]
- data OptDir
- data ObjectiveFunction c = ObjectiveFunction {}
- data Constraint c = Constraint {
- constrLabel :: Maybe Label
- constrIndicator :: Maybe (Var, c)
- constrExpr :: Expr c
- constrLB :: BoundExpr c
- constrUB :: BoundExpr c
- constrIsLazy :: Bool
- (.==.) :: Num c => Expr c -> Expr c -> Constraint c
- (.<=.) :: Num c => Expr c -> Expr c -> Constraint c
- (.>=.) :: Num c => Expr c -> Expr c -> Constraint c
- data RelOp
- data SOSType
- data SOSConstraint c = SOSConstraint {}
- data Solution r = Solution {
- solStatus :: Status
- solObjectiveValue :: Maybe r
- solVariables :: Map Var r
- data Status
- meetStatus :: Status -> Status -> Status
- data Tol r = Tol {
- integralityTol :: r
- feasibilityTol :: r
- optimalityTol :: r
- zeroTol :: Fractional r => Tol r
- class Eval r a where
- data FileOptions = FileOptions {}
- data WriteSetting
- class Default a where
- def :: a
- class Variables a where
- intersectBounds :: Ord c => Bounds c -> Bounds c -> Bounds c
Mixed-Integer Programming (MIP) problem specification
MIP problems
A problem instance
Constructors
| Problem | |
Fields
| |
Instances
| Functor Problem Source # | |
| RealFrac r => Eval r (Problem r) Source # | |
| Variables (Problem c) Source # | |
| Show c => Show (Problem c) Source # | |
| Default (Problem c) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Eq c => Eq (Problem c) Source # | |
| Ord c => Ord (Problem c) Source # | |
| type Evaluated r (Problem r) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
Set of variables
binaryVariables :: (Num c, Eq c) => Problem c -> Set Var Source #
Set of binary variables (integers variables with lower bound 0 and upper bound 1) of a Problem
semiContinuousVariables :: Problem c -> Set Var Source #
Set of semi-continuous variables of a Problem
Variable's attributes
Variables
Variables used in problems
Instances
| Variables Var Source # | |
| IsString Var Source # | |
Defined in Numeric.Optimization.MIP.Base Methods fromString :: String -> Var # | |
| Show Var Source # | |
| Eq Var Source # | |
| Ord Var Source # | |
| Hashable Var Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Num r => Eval r Var Source # | |
| type Evaluated r Var Source # | |
Defined in Numeric.Optimization.MIP.Base | |
toVar :: String -> Var Source #
Deprecated: Use fromString function or Var pattern instead
convert a string into a variable
fromVar :: Var -> String Source #
Deprecated: Use varName function or Var pattern instead
convert a variable into a string
Variable types
Type of variables
Variables can take values depending on their types and their bounds (Bounds).
Constructors
| ContinuousVariable | can take values from \(\{x \in \mathbb{R} \mid L \le x \le U\}\) |
| IntegerVariable | can take values from \(\{x \in \mathbb{Z} \mid L \le x \le U\}\) |
| SemiContinuousVariable | can take values from \(\{0\} \cup \{x \in \mathbb{R} \mid L \le x \le U\}\) |
| SemiIntegerVariable | can take values from \(\{0\} \cup \{x \in \mathbb{Z} \mid L \le x \le U\}\) |
Variable bounds
Extended r is an extension of r with positive/negative infinity (±∞).
Instances
| Functor Extended | |
| Data r => Data (Extended r) | |
Defined in Data.ExtendedReal Methods gfoldl :: (forall d b. Data d => c (d -> b) -> d -> c b) -> (forall g. g -> c g) -> Extended r -> c (Extended r) # gunfold :: (forall b r0. Data b => c (b -> r0) -> c r0) -> (forall r1. r1 -> c r1) -> Constr -> c (Extended r) # toConstr :: Extended r -> Constr # dataTypeOf :: Extended r -> DataType # dataCast1 :: Typeable t => (forall d. Data d => c (t d)) -> Maybe (c (Extended r)) # dataCast2 :: Typeable t => (forall d e. (Data d, Data e) => c (t d e)) -> Maybe (c (Extended r)) # gmapT :: (forall b. Data b => b -> b) -> Extended r -> Extended r # gmapQl :: (r0 -> r' -> r0) -> r0 -> (forall d. Data d => d -> r') -> Extended r -> r0 # gmapQr :: forall r0 r'. (r' -> r0 -> r0) -> r0 -> (forall d. Data d => d -> r') -> Extended r -> r0 # gmapQ :: (forall d. Data d => d -> u) -> Extended r -> [u] # gmapQi :: Int -> (forall d. Data d => d -> u) -> Extended r -> u # gmapM :: Monad m => (forall d. Data d => d -> m d) -> Extended r -> m (Extended r) # gmapMp :: MonadPlus m => (forall d. Data d => d -> m d) -> Extended r -> m (Extended r) # gmapMo :: MonadPlus m => (forall d. Data d => d -> m d) -> Extended r -> m (Extended r) # | |
| Bounded (Extended r) | |
| (Num r, Ord r) => Num (Extended r) | Note that
|
Defined in Data.ExtendedReal | |
| Read r => Read (Extended r) | |
| (Fractional r, Ord r) => Fractional (Extended r) | Note that |
| Show r => Show (Extended r) | |
| NFData r => NFData (Extended r) | |
Defined in Data.ExtendedReal | |
| Eq r => Eq (Extended r) | |
| Ord r => Ord (Extended r) | |
| Hashable r => Hashable (Extended r) | |
Defined in Data.ExtendedReal | |
type Bounds c = (BoundExpr c, BoundExpr c) Source #
type for representing lower/upper bound of variables
defaultBounds :: Num c => Bounds c Source #
default bounds
Labels
Expressions
Arithmetic expressions
Essentialy an expression is a sequence of Terms.
terms
Objective function
The OptDir type represents optimization directions.
Instances
| Data OptDir | |
Defined in Data.OptDir Methods gfoldl :: (forall d b. Data d => c (d -> b) -> d -> c b) -> (forall g. g -> c g) -> OptDir -> c OptDir # gunfold :: (forall b r. Data b => c (b -> r) -> c r) -> (forall r. r -> c r) -> Constr -> c OptDir # toConstr :: OptDir -> Constr # dataTypeOf :: OptDir -> DataType # dataCast1 :: Typeable t => (forall d. Data d => c (t d)) -> Maybe (c OptDir) # dataCast2 :: Typeable t => (forall d e. (Data d, Data e) => c (t d e)) -> Maybe (c OptDir) # gmapT :: (forall b. Data b => b -> b) -> OptDir -> OptDir # gmapQl :: (r -> r' -> r) -> r -> (forall d. Data d => d -> r') -> OptDir -> r # gmapQr :: forall r r'. (r' -> r -> r) -> r -> (forall d. Data d => d -> r') -> OptDir -> r # gmapQ :: (forall d. Data d => d -> u) -> OptDir -> [u] # gmapQi :: Int -> (forall d. Data d => d -> u) -> OptDir -> u # gmapM :: Monad m => (forall d. Data d => d -> m d) -> OptDir -> m OptDir # gmapMp :: MonadPlus m => (forall d. Data d => d -> m d) -> OptDir -> m OptDir # gmapMo :: MonadPlus m => (forall d. Data d => d -> m d) -> OptDir -> m OptDir # | |
| Bounded OptDir | |
| Enum OptDir | |
Defined in Data.OptDir | |
| Generic OptDir | |
| Ix OptDir | |
| Read OptDir | |
| Show OptDir | |
| NFData OptDir | |
Defined in Data.OptDir | |
| Eq OptDir | |
| Ord OptDir | |
| Hashable OptDir | |
Defined in Data.OptDir | |
| type Rep OptDir | |
data ObjectiveFunction c Source #
objective function
Instances
Constraints
Linear (or Quadratic or Polynomial) constraints
data Constraint c Source #
Constraint
In the most general case, it is of the form x = v → L ≤ e ≤ U.
Constructors
| Constraint | |
Fields
| |
Instances
relational operators
SOS constraints
types of SOS (special ordered sets) constraints
Instances
| Enum SOSType Source # | |
| Read SOSType Source # | |
| Show SOSType Source # | |
| Eq SOSType Source # | |
| Ord SOSType Source # | |
Defined in Numeric.Optimization.MIP.Base | |
data SOSConstraint c Source #
SOS (special ordered sets) constraints
Instances
Solutions
Type for representing a solution of MIP problem.
Constructors
| Solution | |
Fields
| |
Instances
| Functor Solution Source # | |
| Show r => Show (Solution r) Source # | |
| Default (Solution r) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Eq r => Eq (Solution r) Source # | |
| Ord r => Ord (Solution r) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
MIP status with the following partial order:
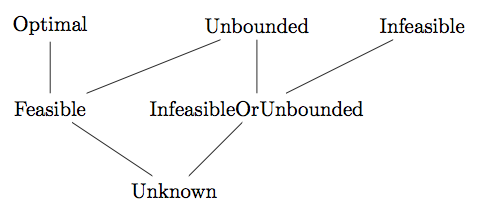
Constructors
| StatusUnknown | |
| StatusFeasible | |
| StatusOptimal | |
| StatusInfeasibleOrUnbounded | |
| StatusInfeasible | |
| StatusUnbounded |
meetStatus :: Status -> Status -> Status Source #
meet (greatest lower bound) operator of the partial order of Status type.
If the version of lattices is <2, then MeetSemiLattice instance can also be used.
Evaluation
Tolerance for evaluating solutions against Problem.
Constructors
| Tol | |
Fields
| |
Instances
| Fractional r => Default (Tol r) Source # | Defautl is |
Defined in Numeric.Optimization.MIP.Base | |
Type class for evaluation various elements of Problem under
the given variable assignments.
Methods
eval :: Tol r -> Map Var r -> a -> Evaluated r a Source #
Evaluate a value of type a under given assignments and the tolerance
Instances
| Num r => Eval r Var Source # | |
| (Num r, Ord r) => Eval r (Constraint r) Source # | |
Defined in Numeric.Optimization.MIP.Base Associated Types type Evaluated r (Constraint r) Source # Methods eval :: Tol r -> Map Var r -> Constraint r -> Evaluated r (Constraint r) Source # | |
| Num r => Eval r (Expr r) Source # | |
| Num r => Eval r (ObjectiveFunction r) Source # | |
Defined in Numeric.Optimization.MIP.Base Associated Types type Evaluated r (ObjectiveFunction r) Source # Methods eval :: Tol r -> Map Var r -> ObjectiveFunction r -> Evaluated r (ObjectiveFunction r) Source # | |
| RealFrac r => Eval r (Problem r) Source # | |
| (Num r, Ord r) => Eval r (SOSConstraint r) Source # | |
Defined in Numeric.Optimization.MIP.Base Associated Types type Evaluated r (SOSConstraint r) Source # Methods eval :: Tol r -> Map Var r -> SOSConstraint r -> Evaluated r (SOSConstraint r) Source # | |
| Num r => Eval r (Term r) Source # | |
File I/O
data FileOptions Source #
Options for reading/writing problem files
Constructors
| FileOptions | |
Fields
| |
Instances
| Show FileOptions Source # | |
Defined in Numeric.Optimization.MIP.Base Methods showsPrec :: Int -> FileOptions -> ShowS # show :: FileOptions -> String # showList :: [FileOptions] -> ShowS # | |
| Default FileOptions Source # | |
Defined in Numeric.Optimization.MIP.Base Methods def :: FileOptions # | |
data WriteSetting Source #
Options for writing something of not
Constructors
| WriteAlways | |
| WriteIfNotDefault | |
| WriteNever |
Instances
Utilities
A class for types with a default value.
Minimal complete definition
Nothing
Instances
class Variables a where Source #
Type class for types that contain variables.
Instances
| Variables Var Source # | |
| Variables (Constraint c) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Variables (Expr c) Source # | |
| Variables (ObjectiveFunction c) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Variables (Problem c) Source # | |
| Variables (SOSConstraint c) Source # | |
Defined in Numeric.Optimization.MIP.Base | |
| Variables (Term c) Source # | |
| Variables a => Variables [a] Source # | |
| (Variables a, Variables b) => Variables (Either a b) Source # | |